|
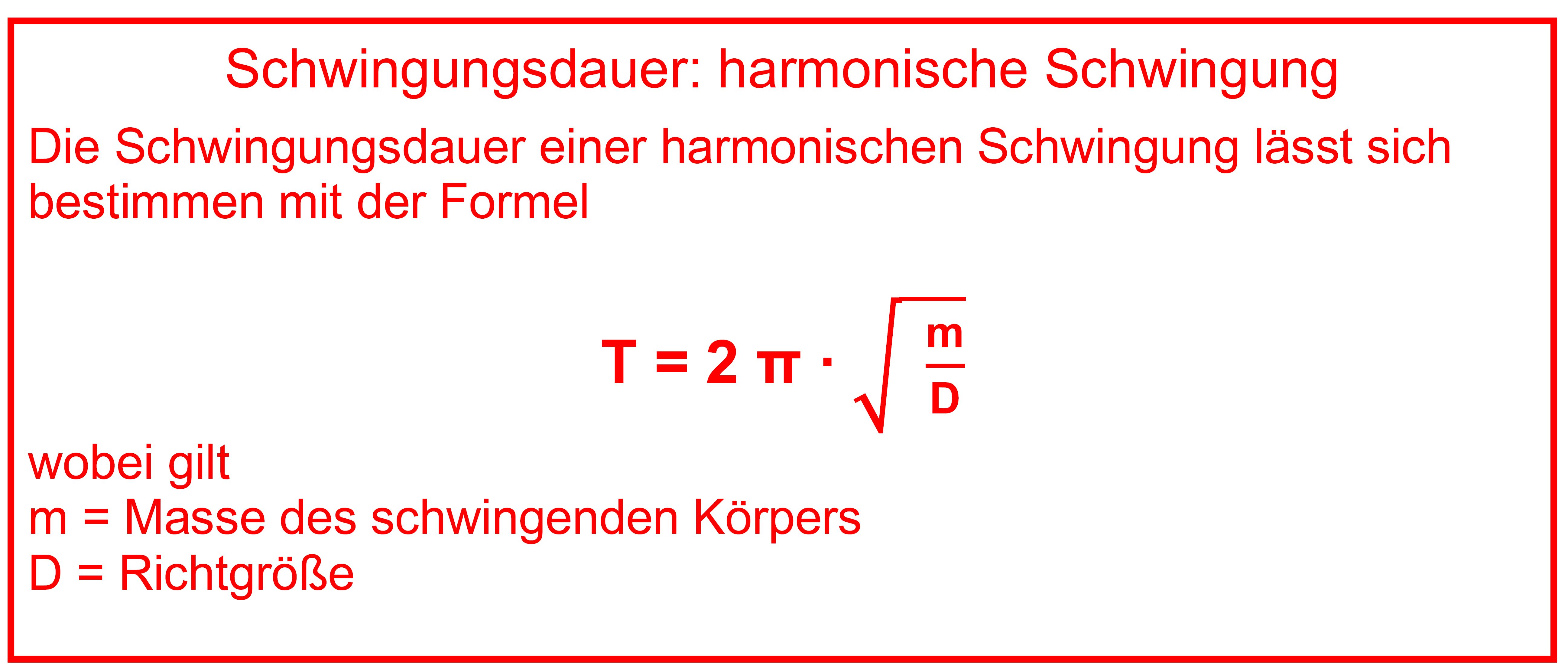
Schwingungsdauer – Q1 Um die Formel für die Schwingungsdauer in der
Q1 herzuleiten, kann man einen deutlich
mathematischer orientierten Weg gehen, da hier schon umfangreiche Kenntnisse aus der
Analysis vorliegen. Es kann aber nichts schaden, sich die Ausführungen für die E-Phase
anzusehen, da hier vor allem auch dargestellt wird, dass ein Zusammen- hang zwischen „Harmonischer Schwingung“ und „Kreisbewegung“ be- steht. Es werden also zwei Themenbereich der
Physik miteinander ver- knüpft. Wir beginnen mit der Grundgleichung der
Mechanik F = m ∙ a und kom- men dann mit Hilfe des
Gesetzes für die harmonische Schwingung FR = − D ∙ s zu einer
Differentialgleichung, die dann gelöst werden wird, um die Bewegungsgleichung zu gewinnen. Mit
Hilfe der Bewegungs- gleichung gelangt man dann zur
Formel für die Schwingungsdauer. Also zunächst einmal zur Bewegungsgleichung:
Wir schauen uns jetzt einmal genauer den
Verlauf der Sinusfunktion an. Da wir für t = 0 s in der Ruhelage starten,
ergibt sich, dass nach t = T = Schwingungsdauer man wieder in der Ruhelage
angekommen sein muss. Es gilt also s (t = 0 s) = s (t = T s) = 0. Beim Sinus ist eine Schwingung (Periode)
durchlaufen, wenn das Argu- ment im Sinus 2 Pi
lautet, d.h. sin (2 Pi) = sin (0) = 0. Es ergibt sich also Folgendes:
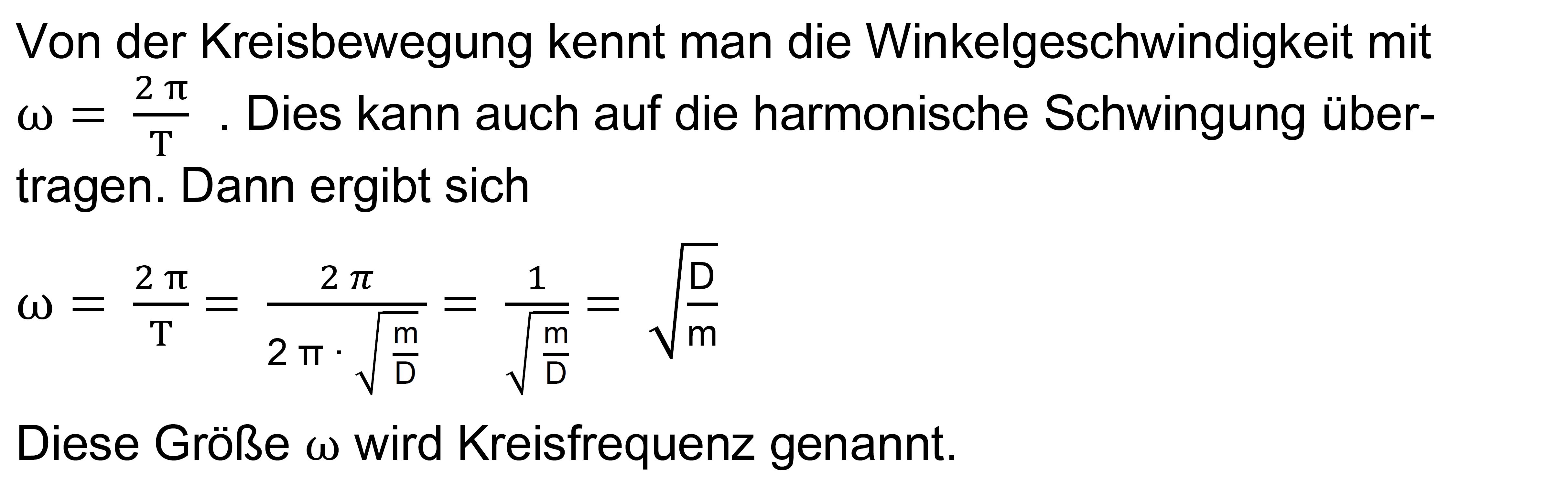
Wenn man sich die Ausführungen für die E-Phase zur Schwingungsdauer und die zur Kreisbewegung ansieht, weiß
man, dass es eine enge Ver- bindung zwischen einer
harmonischen Schwingung und einer gleichför- migen Kreisbewegung gibt.
Mit dieser neuen Größe Kreisfrequenz ergibt
sich jetzt folgende Beweg- ungsgleichung:
Schwingungsdauer:Federpendel und Fadenpendel Die häufigsten harmonischen Schwingungen sind die
Schwingung des Federpendels und des Fadenpendels (bei kleinem
Auslenkungswinkel). Hier kennen wir auch die Richtgröße D. Es gilt:
- zurück zur „Harmonischen Schwingung“ - weiter zur
„Energie einer harmonischen Schwingung“ |