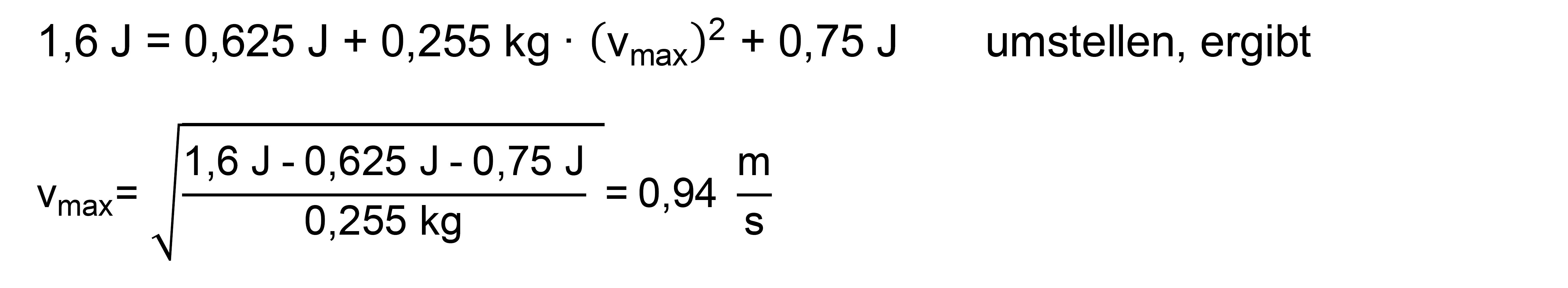|
Energieverhältnisse einer schwingenden
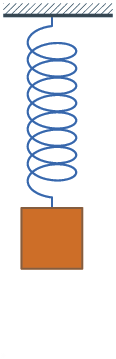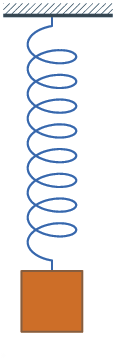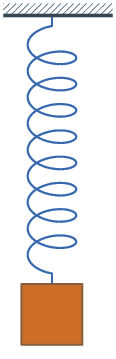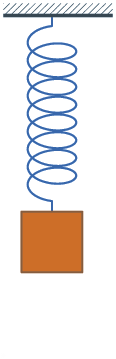
Feder Wenn man an eine entspannte Feder ein
Massestück hängt, wird diese Feder ausgedehnt. Vom Massestück wurde Arbeit
an der Feder verrich- tet. Die Feder hat an
Spannenergie gewonnen. Es stellt sich ein Gleich- gewicht zwischen Federkraft
und Gewichtskraft ein. Das Massestück hängt in Ruhe an der Feder. Man nennt diese
Lage daher „Ruhelage“. Dies ändert sich, wenn man die Feder mit
Muskelkraft noch weiter aus- dehnt und dann loslässt. Die Feder übt jetzt
Schwingungen aus, die sym- metrisch zur Ruhelage verlaufen. In der Ruhelage
haben wir jetzt die grö- ßte Geschwindigkeit. Vom
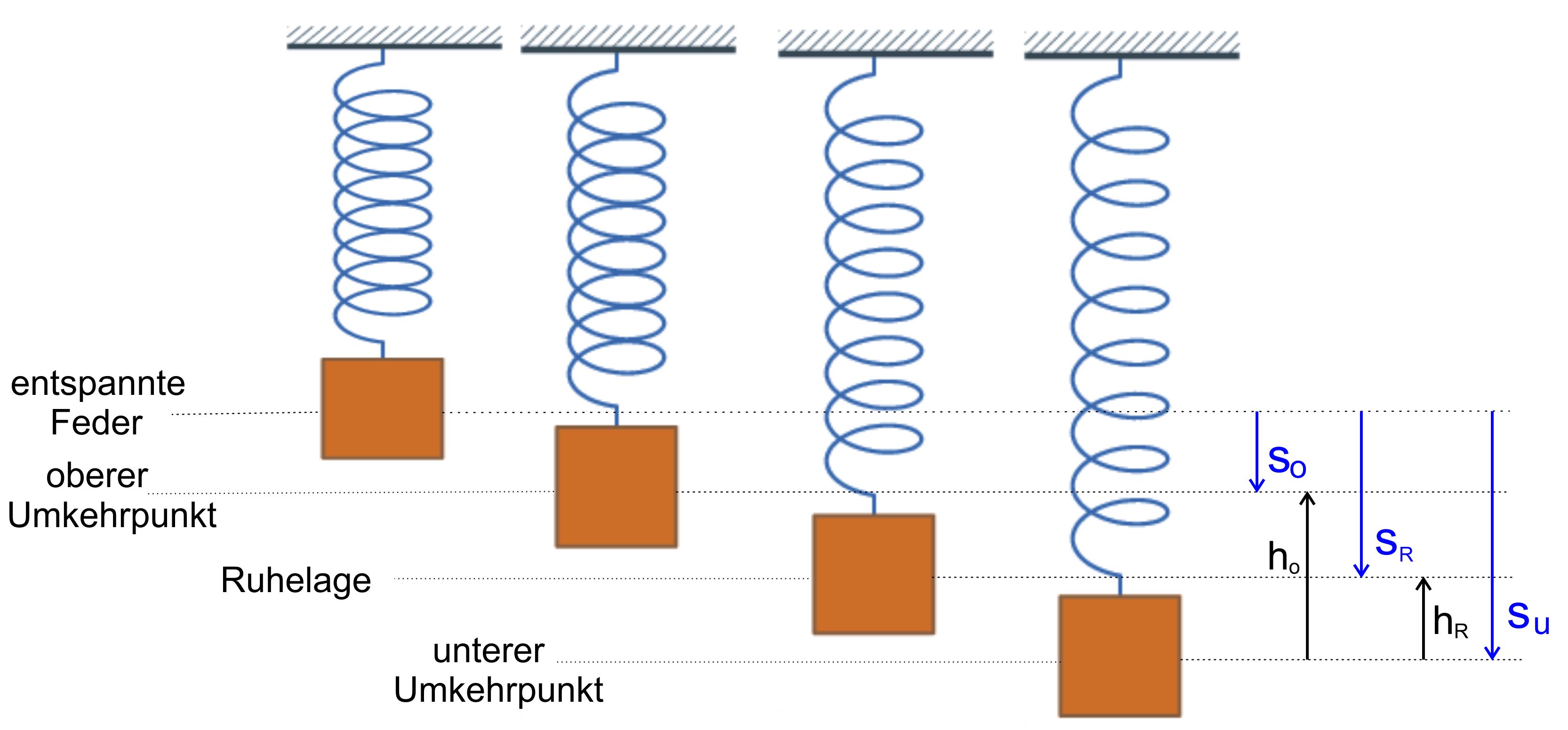
untersten Punkt (dem unteren Umkehrpunkt) aus wird die Masse bis zur Ruhelage hin
beschleunigt und danach abge- bremst bis sie im oberen Umkehrpunkt zur Ruhe
kommt. Danach beginnt der Vorgang von vorne, nur in der
entgegensetzten Richtung. Das sieht dann so aus.
https://commons.wikimedia.org/wiki/File:Simple_harmonic_oscillator.gif Hier noch einmal die Verhältnisse in einer
Abbildung:
Komplexer
Ansatz zu den Energieverhältnissen: Die verrichtete Arbeit bestand zunächst aus
Spannarbeit, die zunächst vom Massestück verrichtet wurde. Zu dieser
ersten Spannarbeit kam dann noch die Spannarbeit durch Muskelkraft
hinzu. Wir verlassen das System am unteren
Umkehrpunkt. Die gesamte Spannarbeit ist jetzt im System, also in der
Feder, als Spannenergie gespeichert. Dies ist somit die Gesamtenergie
des Systems, die nicht mehr verloren geht. Dieser Energiewert kann
nur umgewandelt werden in kinetische Energie (wenn eine Bewegung
auftritt) oder in potentielle Energie, wenn das Massestück an Höhe gewinnt. Schauen wir uns mal die einzelnen Positionen
an. unterer
Umkehrpunkt: maximale Ausdehnung der Feder, keine
Geschwindigkeit, keine Höhe (außer der Höhe über der Erdoberfläche, diese
kann man aber unbe- rücksichtigt lassen, da die sich
während der Schwingung nicht ändert; oder andere Betrachtung: man legt den unteren
Umkehrpunkt genau auf die Erdoberfläche; oder weitere
Überlegung: nur die Höhenänder- ung ist wichtig bei den
Energieumwandlungen). Wir halten also fest: s = maximal; v = 0 m/s; h = 0 m d.h. Energie =
maximale Spannenergie Ruhelage: Feder hat
sich entspannt, nicht mehr so weit gedehnt;
Geschwindigkeit ist maximal, Höhe hat zugenommen. Energie =
mittlere Spannenergie + größte kinetische Energie + mittlere potentielle
Energie oberer
Umkehrpunkt: Feder hat sich weiter entspannt, ist aber
noch ausgedehnt; keine Ge- schwindigkeit; größte Höhe. Energie = kleinste Spannenergie + maximale
potentielle Energie alle
weiteren Punkte Es gibt im
Allgemeinen immer: Energie =
Spannenergie + kinetische Energie + potentielle Energie Jetzt einmal
in Formelschreibweise: Benutzt
werden die Benennungen aus der Abbildung (blaue Angaben)
Beispielaufgabe
Einfacher
Ansatz zu den Energieverhältnissen: In dem
Kapitel zu den „Harmonischen Schwingungen“
haben wir schon hergeleitet,
dass die Gewichtskraft und die Federkraft zusammen die Rückstellkraft
der Schwingung bilden. Für den
Betrag der Rückstellkraft gilt: FR
= D ∙ s (s = Elongation = „ Abstand zur
Ruhelage“) Um die
Auslenkenergie („potentielle Energie“) des harmonischen Schwingers
zu berechnen, muss man wieder das Kraft-Weg-Diagramm ansehen, da
FR nicht konstant ist. Wir können
also wie im Kapitel „Spannarbeit“ vorgehen. Somit ergibt
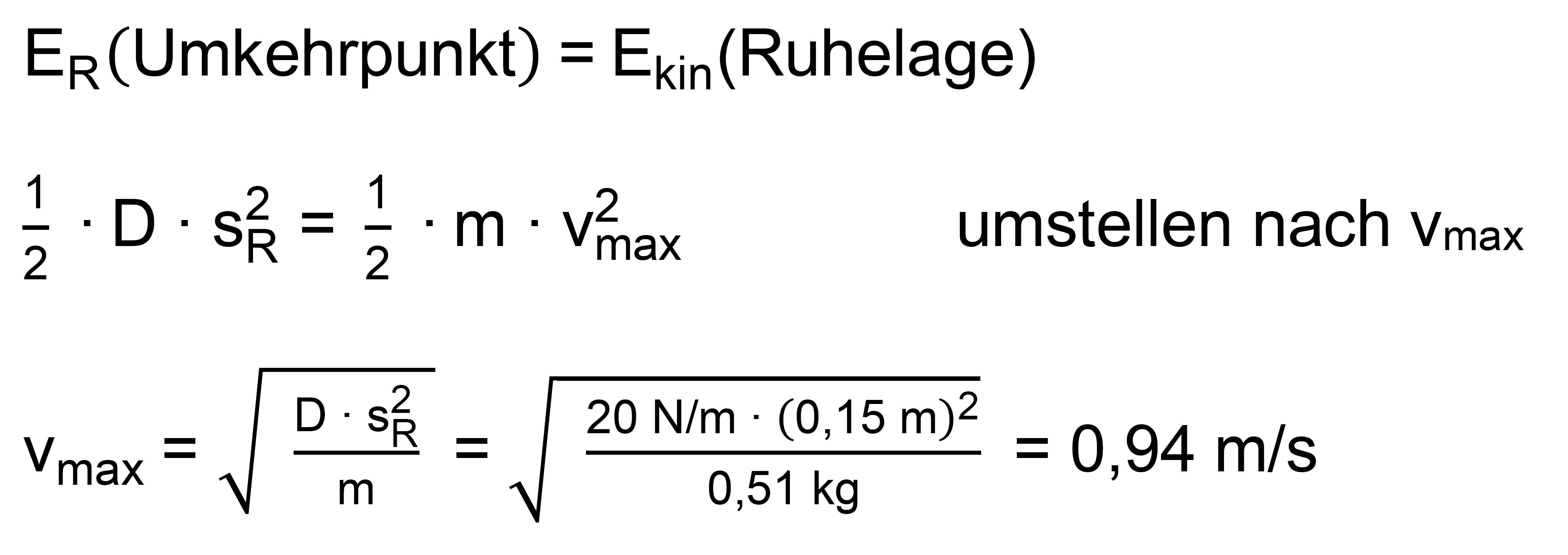
sich für die Auslenkenergie des harmonischen Schwin- gers:
ER
beinhaltet jetzt alle potentiellen Energien (Spannenergie + Lage- energie) vom oberen
komplexen Fall. Die
Gesamtenergie eines harmonischen Schwingers besteht dann aus dieser Auslenkungsenergie
und der kinetischen Energie.
Hiermit
lässt sich das Beispiel von oben ganz einfach rechnen. Die Auslenkungsenergie
ist ja verantwortlich für die Bewegung.
|