Schiefe Ebene

Unter einer schiefen Ebene versteht man eine schräg nach oben ver-

laufende Ebene. Im Alltag wäre dies eine Rampe oder eine Fahrbahn

(Serpentinen), die schräg nach oben verläuft. Schöne Beispiele findet

man in diesem Link bei Wikipedia:

Welche Kräfte wirken auf eine Masse, die sich auf einer schiefen Ebe-

ne befindet, unter der Annahme, dass ein reibungsfreier Fall vorliegt.

Im reibungsfreien Fall gibt es also keine Reibungskraft zwischen Kör-

per und Ebene, d.h.der Körper wird immer die schiefe Ebene hinunter-

gleiten (Rotation soll nicht vorliegen).

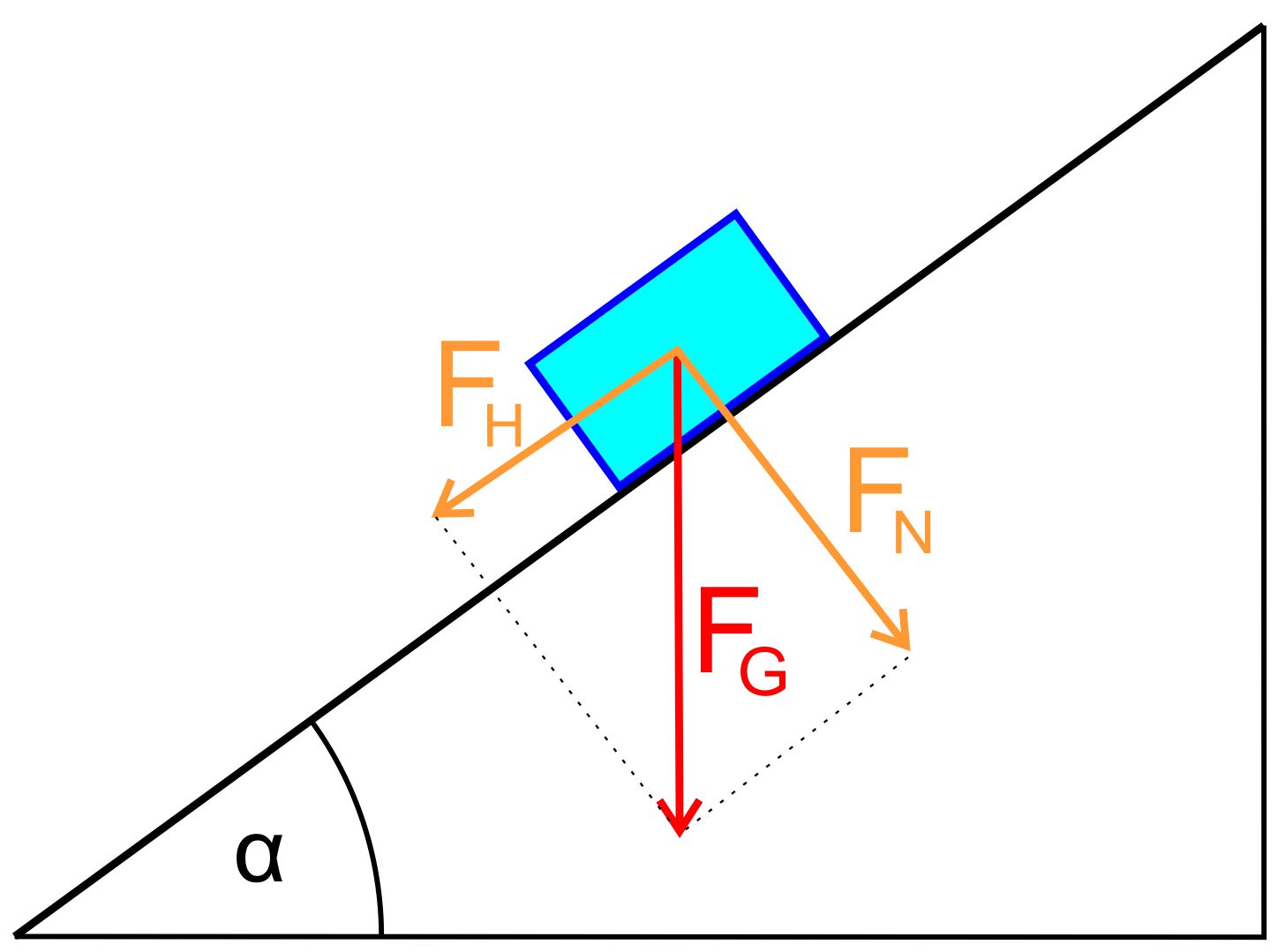
Die Kräfteverhältnisse werden in der folgenden Abbildung (vereinfacht)

gezeigt:

Es wirkt nur die Gewichtskraft zum Erdmittelpunkt (s. Hinweis unten). Man

muss jetzt überlegen, welche Auswirkungen diese Kraft in die interes-

santen Richtungen hat. Man macht eine Komponentenzerlegung, d.h.

es muss ein Kräfteparallelogramm erstellt werden. Man ist immer da-

ran interessiert zu wissen, wie die Gleitbewegung nach unten erfolgt,

also ist diese Richtung wichtig und die eine Kraftkomponente sollte da-

her in Bewegungsrichtung, also parallel zur Ebene, zeigen. Diese

Komponente nennt man häufig „Hangabtriebskraft“ und wählt dafür F_H.

Die zweite Komponente sollte jetzt keine Auswirkungen in dieser Be-

wegungsrichtung haben; daher muss die zweite Komponente für das

Kräfteparallelogramm senkrecht zur interessanten Richtung stehen.

Deshalb wird sie häufig Normalkraft F_N (besser Normalkomponente der Gewichtskraft) genannt. Die Abbildung zeigt die entsprechende Zerlegung.

Hinweis: Dies ist eine nicht völlig korrekte Darstellung, da eigentlich noch die Kraft eingefügt

werden muss, die von der schiefen Ebene F_U (Unterlage) auf den Körper ausgeübt wird. Es

ergeben sich sonst Widersprüche zum „ Zweiten Axiom von Newton“. Korrekte Darstellungen

finden sich in den Büchern von Tipler und Giancoli. Man kann sich auch die herbe Kritik von

Prof. Maurer ansehen. Für unsere Betrachtungen ist ja nur die Komponente in Bewegungs-

richtung interessant, da sich die Kraft von der schiefen Ebene als Unterlage und die Normal-

komponente der Gewichtskraft im reibungsfreien Fall gegenseitig aufheben.

Aus der folgenden Abbildung ergeben sich die entsprechenden For-

meln für die Komponenten:

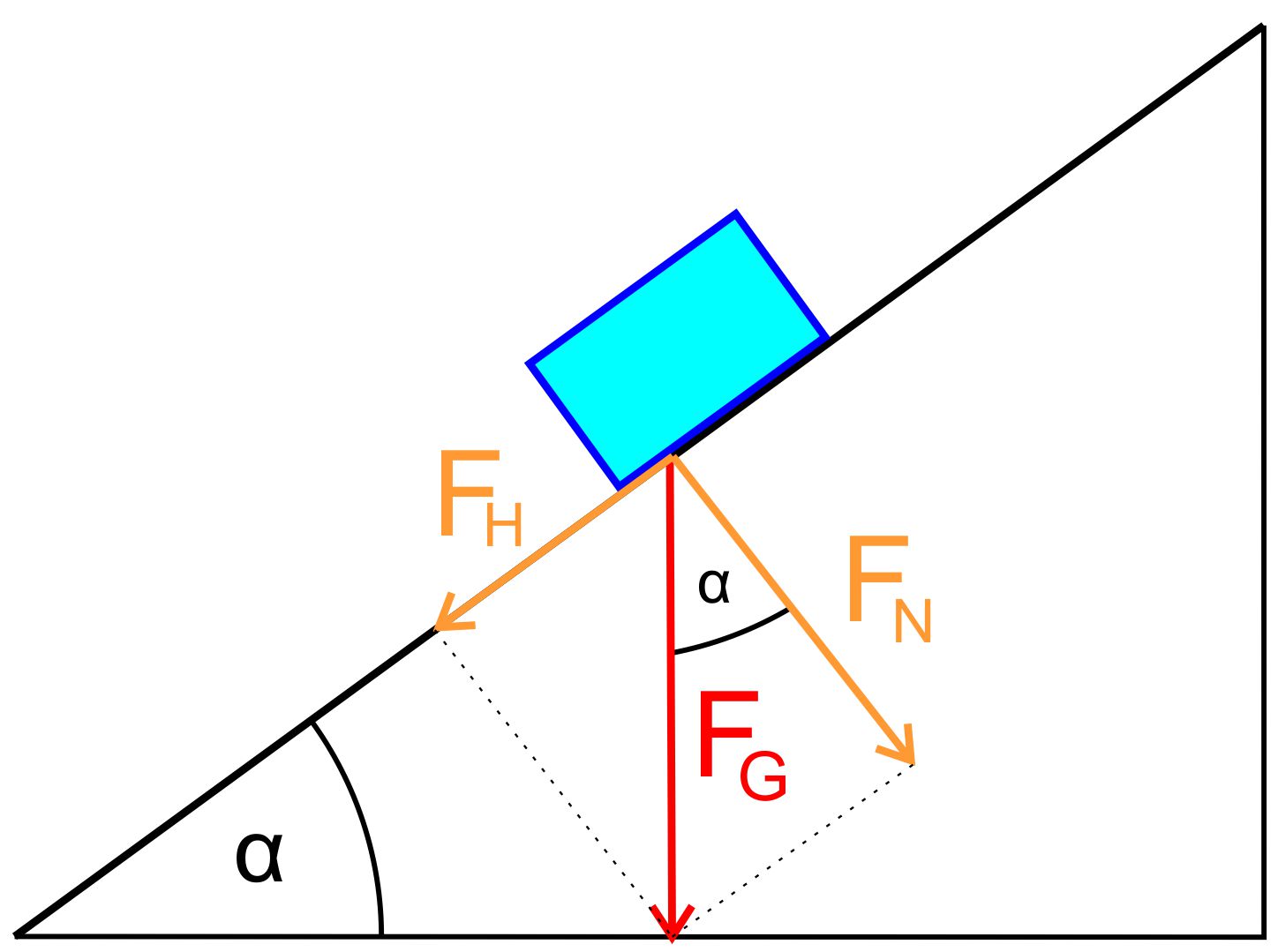
Man hat das Kräfteparallelogramm so verschoben, dass man anhand

der rechtwinkligen Dreiecke gut erkennen kann, dass der Winkel

zwischen F_G und F_N ebenfalls α entspricht.

Formeln zur schiefen Ebene

F_G = m ∙ g ; F_H = m ∙ g ∙ sin(α); F_N = m ∙ g ∙ cos(α)