Arbeit und Energie

 

Die physikalische Größe „Arbeit“

 

Wir orientieren uns hier an der Definition aus der Mittelstufe. Es wird nur eine

vereinfachte Definition benutzt.

 

Wir untersuchen kurz, wie man darauf kommt, diese Größe einzuführen.

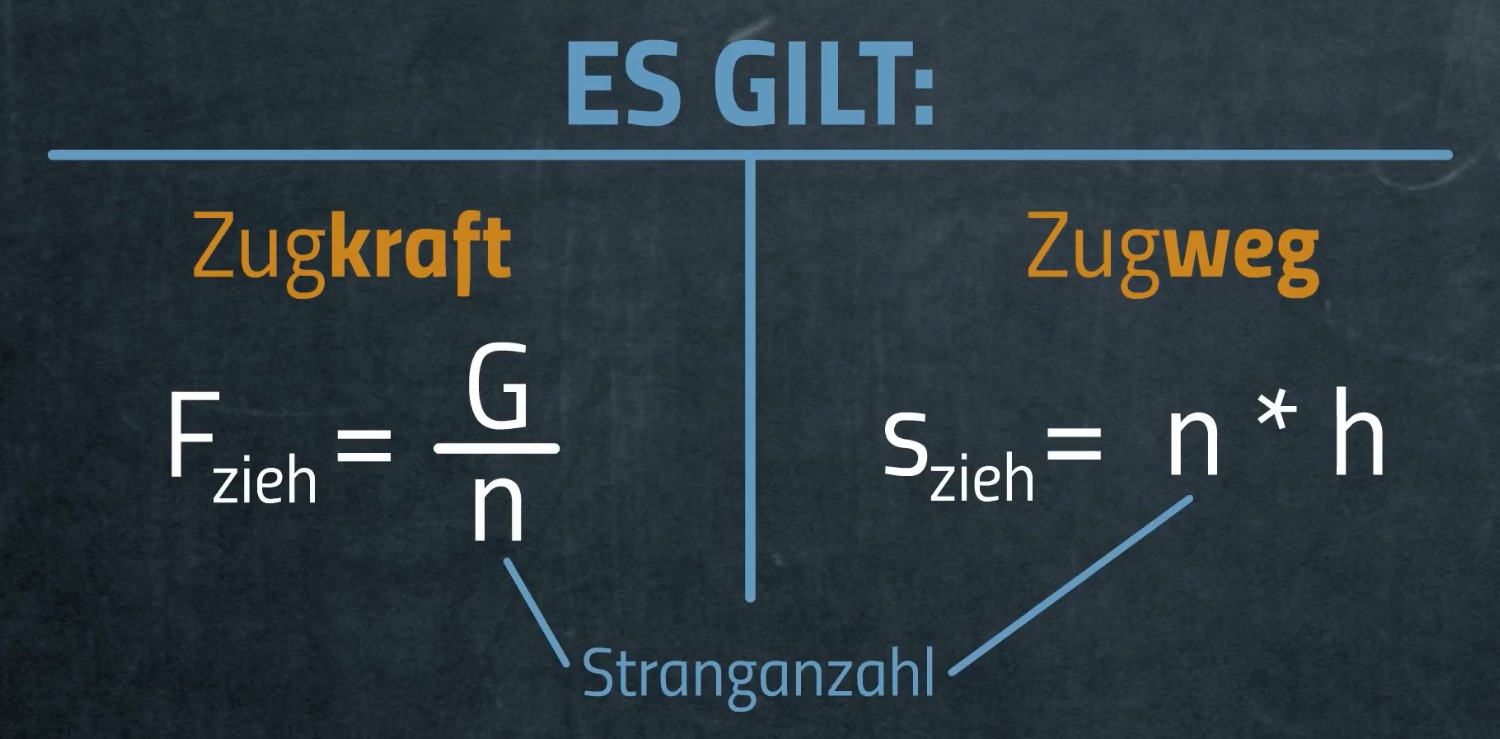
Hierzu sollte man sich mit den einfachen Maschinen beschäftigt haben.

Einfache Maschinen sind z. Bsp. der Flaschenzug, eine schiefe Ebene oder

der Hebel.

Hierzu ein paar Videos (zur Erinnerung).

 

 

In allen Videos (bzw. einfachen Maschinen) spielt das Produkt aus Kraft und

zurückgelegtem Weg eine entscheidende Rolle. Daher wird dieses Produkt be-

sonders definiert. Dieses Produkt bildet nämlich die Größe „Arbeit“.

 

Es gilt also:

 

 

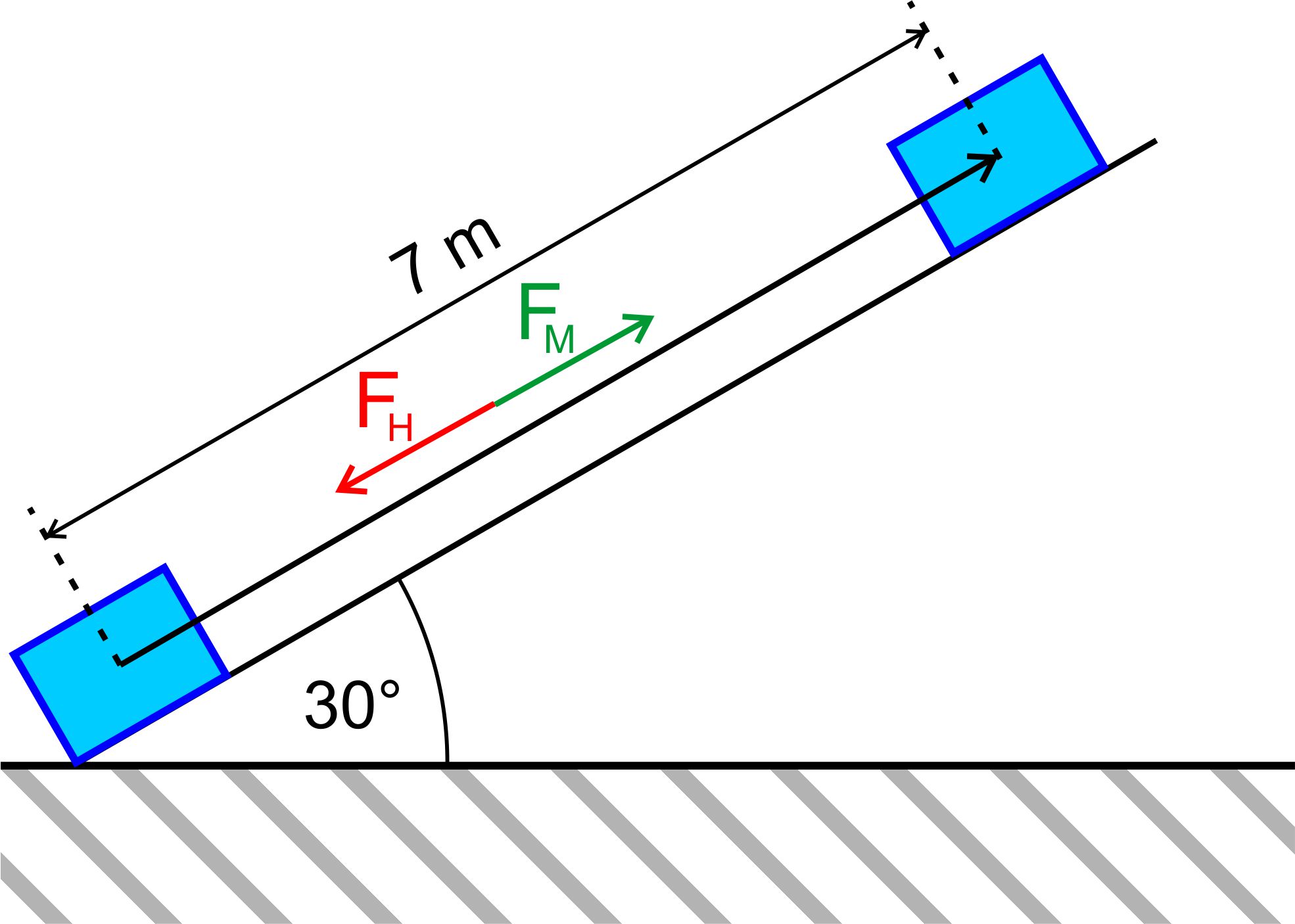
Interessant wird die Formel, wenn die Kraft nicht parallel zum zurückgelegten

Weg liegt.

Hierzu die folgende Abbildung:

 

 

F kann man hier in zwei Komponenten aufteilen. Nur Fs zeigt dabei in Weg-

richtung und ist somit für die Zurücklegung des Weges zuständig.

Die andere Komponente steht senkrecht hierzu und sorgt im Beispiel dafür,

dass die Masse etwas angehoben wird.

 

Für die Berechnung der Arbeit gilt jetzt die angepasste Formel:

 

 

 

Diese einfache Formel gilt nur, wenn die Kraft sich bei der Verrichtung des

Weges nicht ändert.

Hinweis: Im Fall, dass sich die Kraft ändert, ergeben sich komplizierte Linienintegrale.

 

Einfache Beispielaufgabe

 

 

 Aufgabe

 

 Ein Schlitten wird 2,5 km auf einer Schneedecke gezogen. Die Zugkraft

beträgt 15N.  Man zieht in einem Winkel von α = 20° zur Horizontalen.

 Wie groß ist die verrichtete Arbeit?

 

 Lösung

 

 Wir gehen davon aus, dass die Zugkraft immer konstant ist. Dann dürfen wir

die  obige Formel benutzen.

 

 W = F ∙ cos(α) ∙ s = 15 N ∙ cos (20°) ∙ 2500 m = 35238,5 N m

 

 

Komplexere Aufgabe

 

 

 Aufgabe

 

 Man schiebt (oder zieht) reibungsfrei eine Kiste mit der Masse m = 60 kg

eine schiefe Ebene 7 m hinauf. Wie groß ist die Arbeit, die man mindestens

verrichten muss? Die schiefe Ebene hat einen Neigungswinkel α von 30°

 

 

Lösung

 

Zu den Verhältnissen an der schiefen Ebene kann man sich folgenden Link zur  schiefen Ebene ansehen.

Hieraus ergibt sich, dass man mindestens die Hangabtriebskraft als Muskel-

kraft  aufbringen muss, damit sich die Kiste nach oben bewegt. Die Hang-

abtriebskraft ist konstant. Der zurückgelegte Weg beträgt 7 m.

 

W = FH ∙ s = m ∙ g ∙ sin(α) ∙ s  = 60 kg ∙ 9,81 N/kg ∙ sin (30°) ∙ 7 m = 2060,1 N m

 

 

Man sollte folgenden Sonderfall beachten:

Wenn die Kraft senkrecht zum zurückgelegten Weg steht, also cos(α) =

cos (90°) = 0 ist, wird keine Arbeit verrichtet (dies wird vor allem bei der Kreisbewegung wichtig).

 

 

 

Liste von Links: noch keine z.Z.

 

 

 

 

Übungsaufgaben (in Arbeit)

 

 

 

  

Nächstes Kapitel: Besondere Arbeitsformen - Hubarbeit usw.