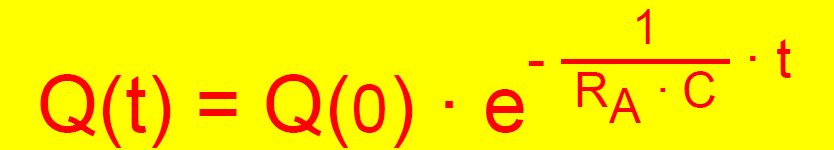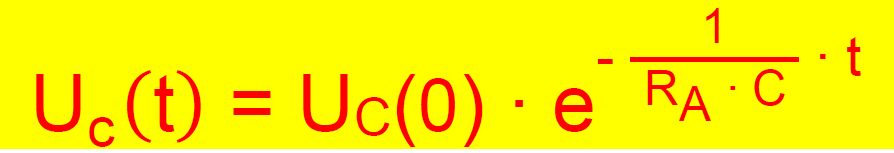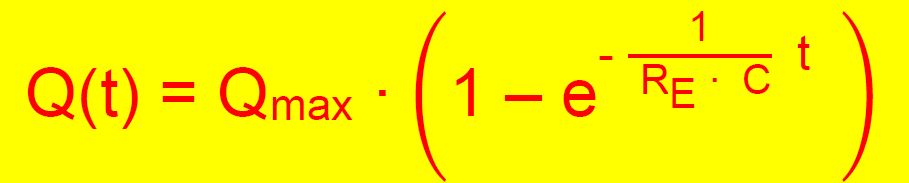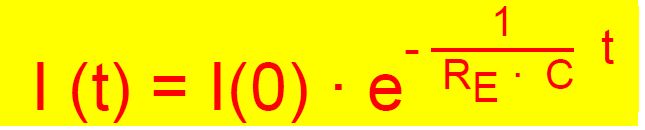|
gehe zu: Kondensator: Auf- und Entladen Einführung Im folgenden Kapitel soll es um einen
Kondensator im Gleichstrom- kreis gehen. Wie verhält sich ein
Kondensator, wenn er an eine Gleichspannungsquelle angeschlossen wird? Was
passiert, wenn die Quelle ausgeschaltet wird? Anschaulich dürfte klar sein, dass beim
Einschalten die Ladungsträger auf die Platten auffließen,
zunächst wohl schnell und dann langsamer. Dies liegt daran, dass zunächst ja keine
Ladungsträger vorliegen, da- nach aber die schon aufgeflossenen
Ladungsträger die weitere Zufuhr behindern. Beim Ausschalten ist es genauso.
Die Abstoßung ist groß. Es gibt viele Ladungen auf den Platten. Es
fließen viel Ladungen ab. Mit der Zeit nimmt die Stromstärke ab, da weniger
Ladungen vorliegen. Hierzu einmal folgende Abbildungen, welche
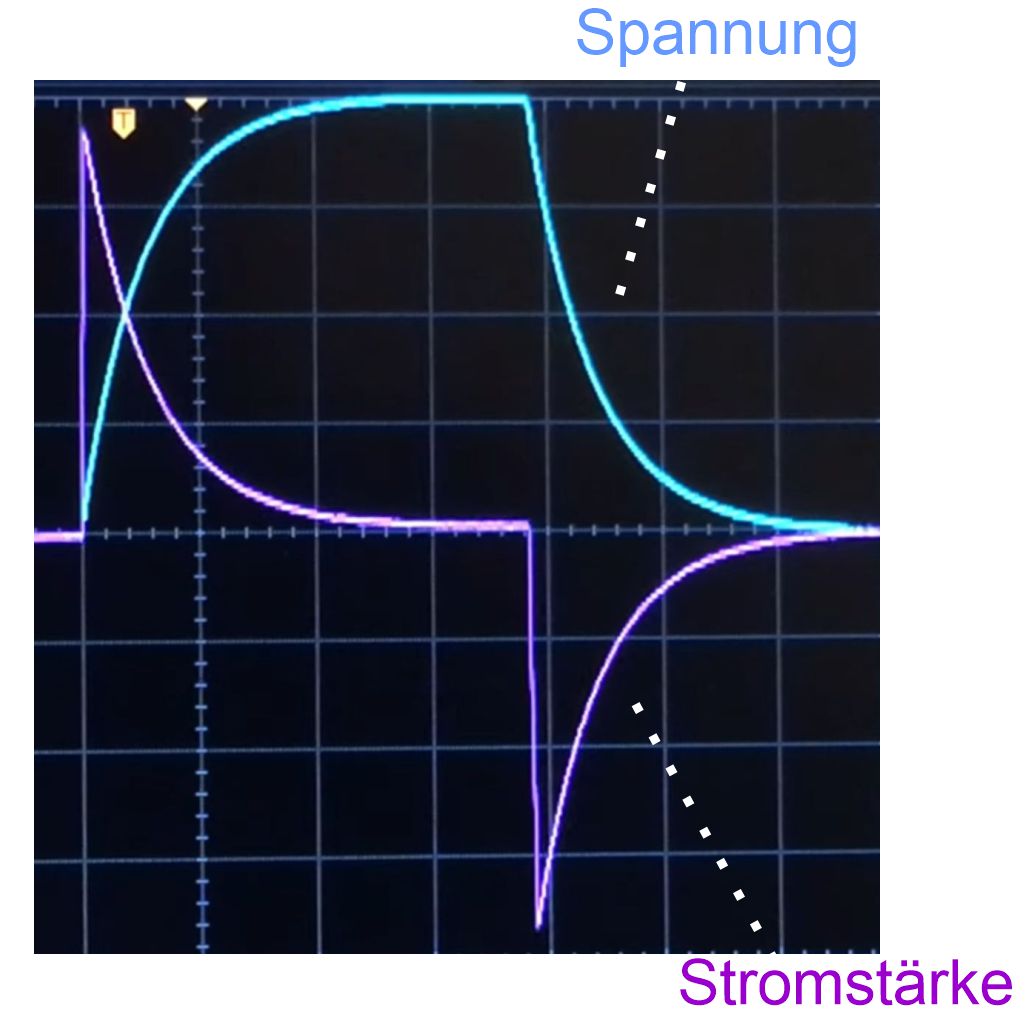
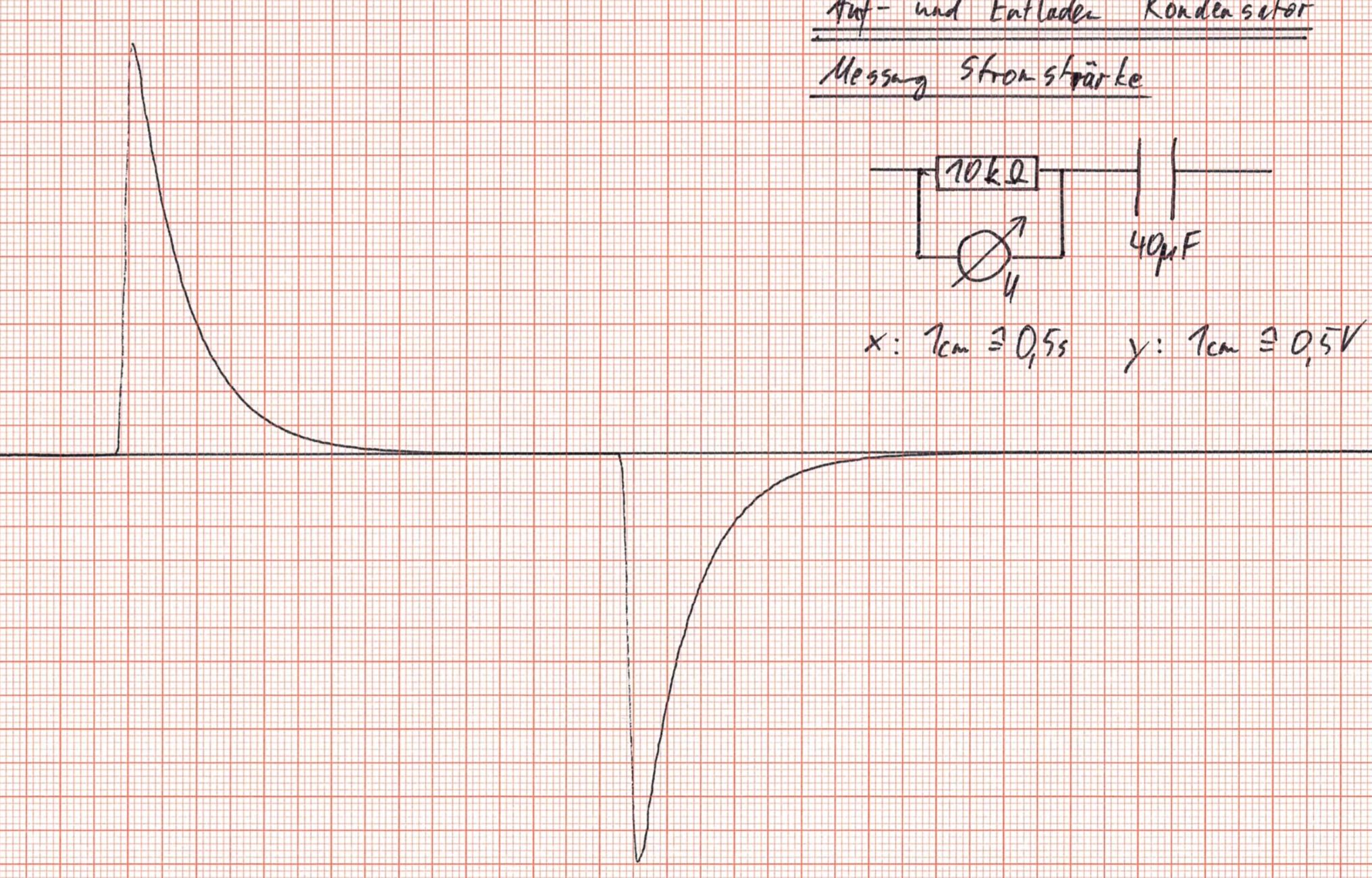
den Stromstärkeverlauf zeigen, einmal auf dem Oszilloskop und mit
einem x-y−Schreiber. Für die Spannung am Kondensator gilt: UC(t)
= Q(t)/C . Dies bedeutet (da C konstant ist), dass die
Spannung von der Ladungsmenge (Anzahl der Ladungen) auf den
Platten abhängt. Beim Aufladen ist diese zunächst gering,
nimmt aber dann ein Maximum an. Beim Entladen haben wir zunächst
ein Maximum von Q, welches dann beim Abfließen aber abnimmt.
Dies stimmt mit dem Spannungsverlauf (s. links) überein. Herleitung
der Funktion für die Verläufe Man kann schon an den Messwerten sehen, dass
es sich wohl um einen exponentiellen Verlauf handeln muss. Es
besteht ein enger Zusammenhang zum Ein- und
Ausschalten von Spulen im Stromkreis.
Wir werden uns an den mathematischen Ausführungen bei den Spulen
orientieren (Einschalten
Spule, Ausschalten
Spule). Zunächst müssen wir uns um die Lösung von
Differentialgleichungen (DGL) kümmern. Hierzu wird bei den Spulen
Folgendes hergeleitet.
Die Herleitung
kann man sich also bei den Spulen noch einmal an- sehen. Es handelt sich übrigens um eine
homogene DGL 1. Ordnung mit konstanten Koeffizienten. Für die folgenden Ausführungen orientieren
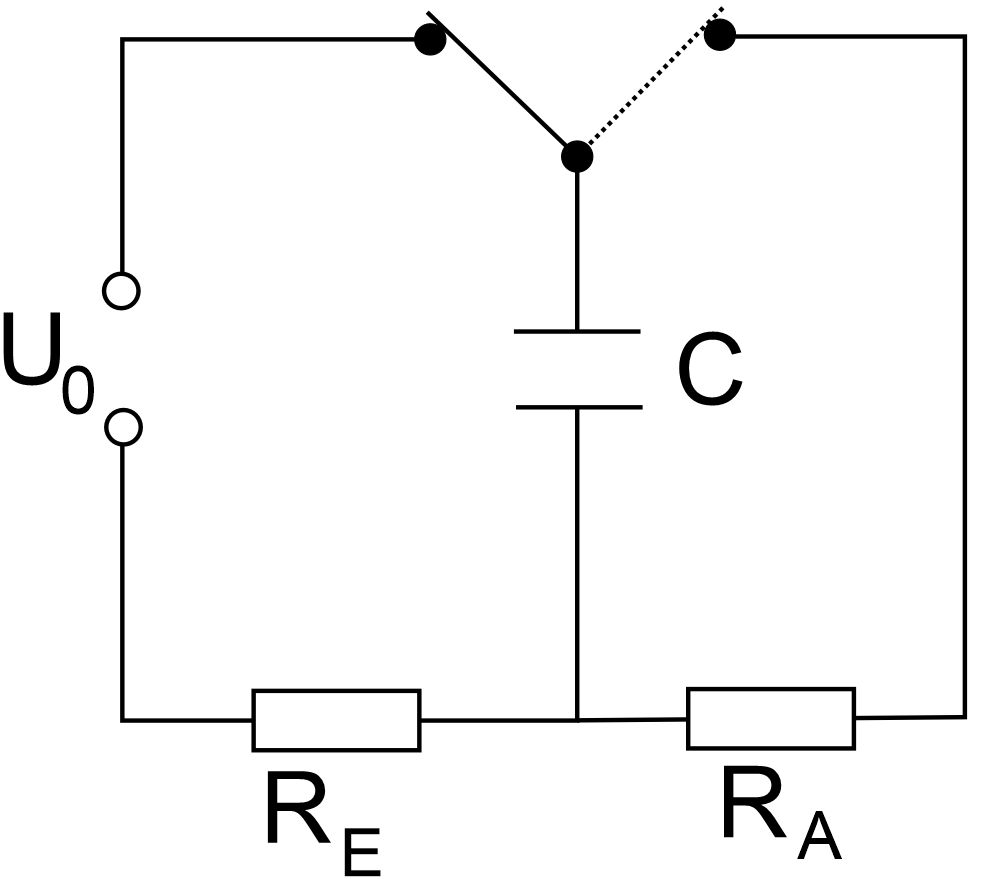
wir uns an dieser Schalt- skizze: Zunächst laden wir den Kondensator C auf.
Legen dann Schalter um, so dass der Kondensator sich entlädt. Der
Entladevorgang ist etwas einfacher zu beschreiben als das Aufladen, so
dass wir damit be- ginnen. Entladevorgang
Zusammenfassung-Entladung
Aufladevorgang
Zusammenfassung-Aufladung
Ergänzung
zur Entladung
Für die Zusammenfassung gilt dann: Zusammenfassung-Entladung
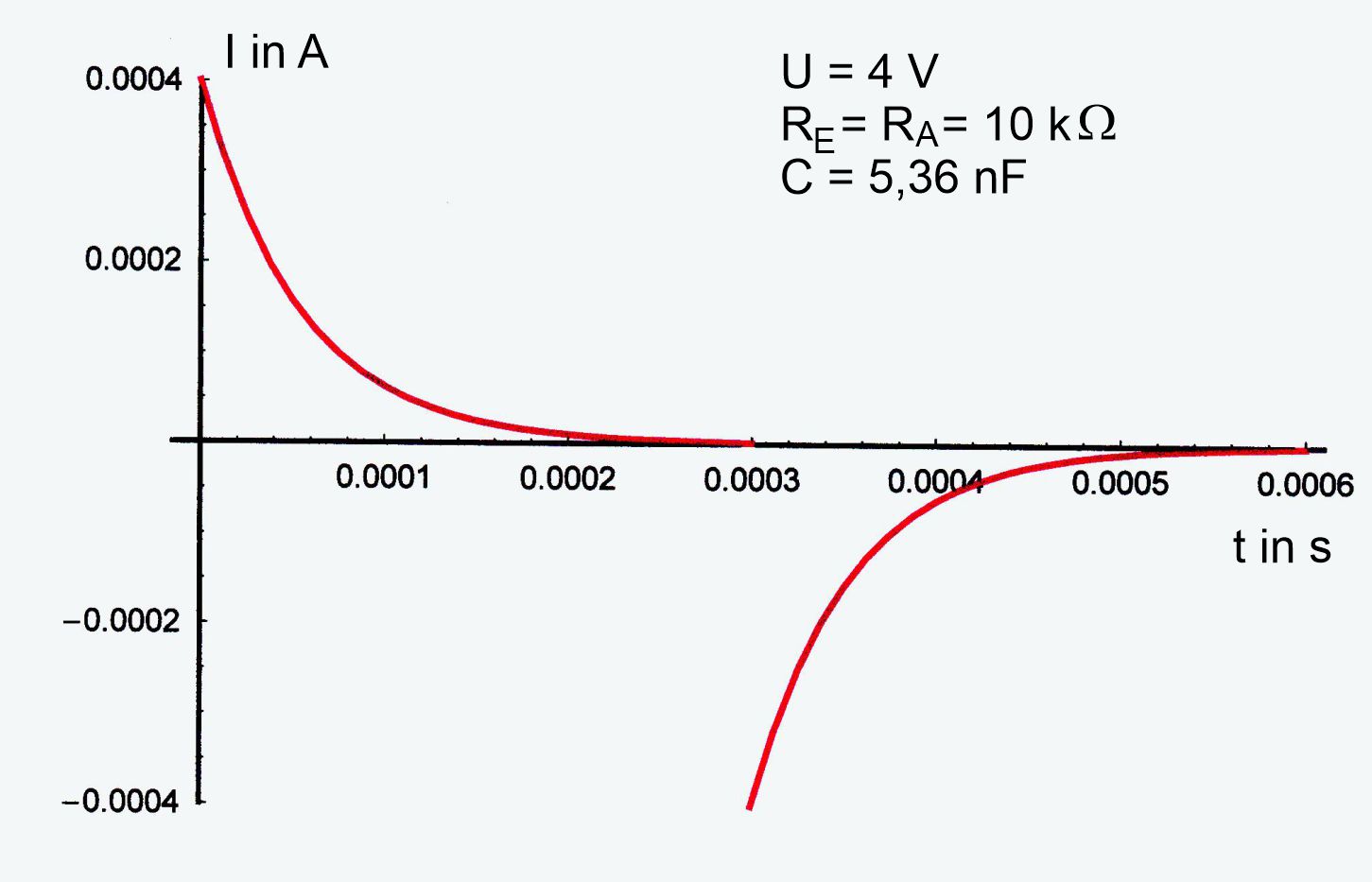
Diagramme Im Folgenden sieht man ein paar Diagramme zur
Stromstärke und zur Spannung. Es wird erst eingeschaltet und
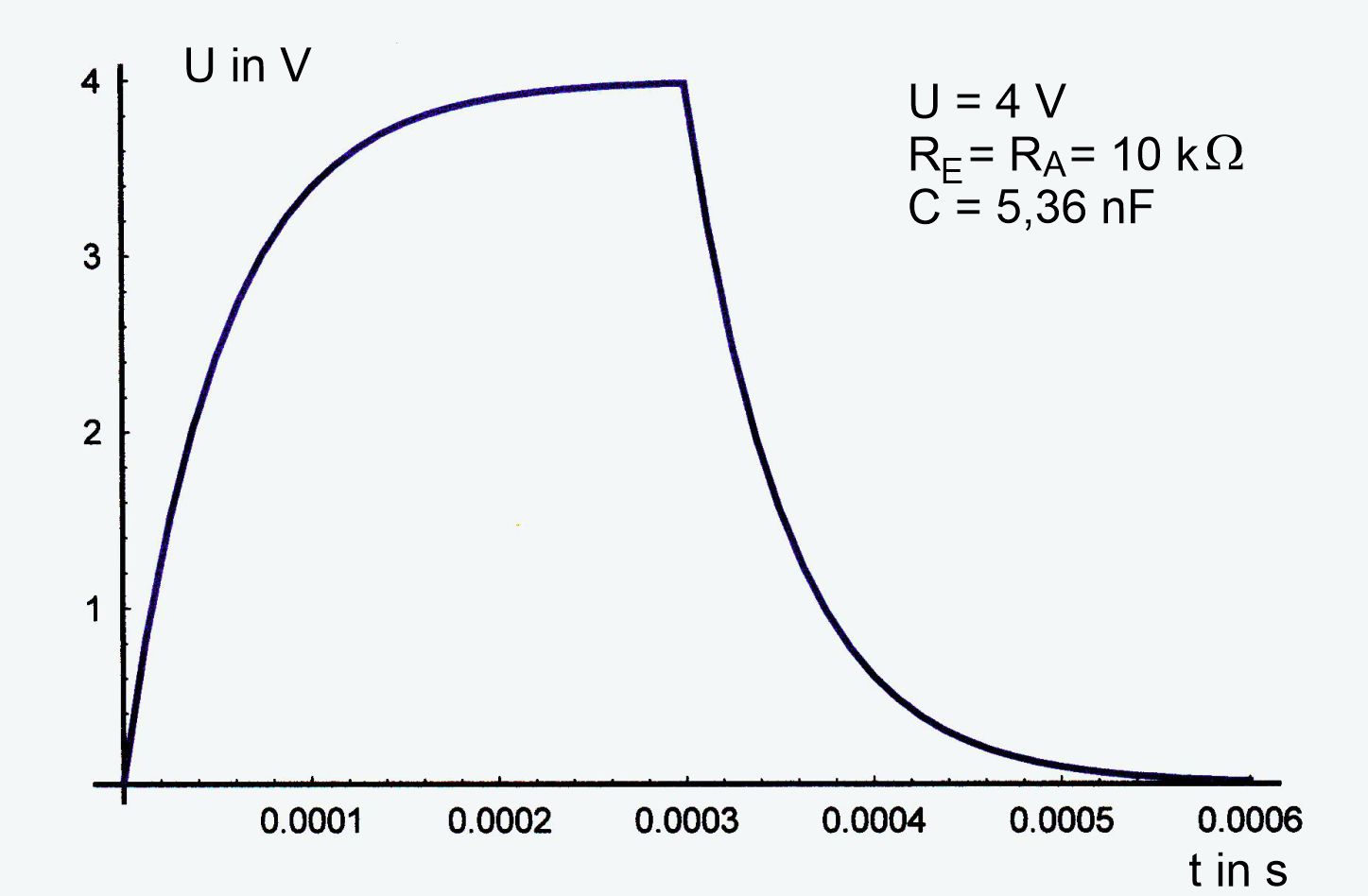
dann ausgeschaltet. 1. Fall: Ein- und Ausschaltwiderstand sind
gleich groß. Man erhält einen symmetrischen Verlauf.
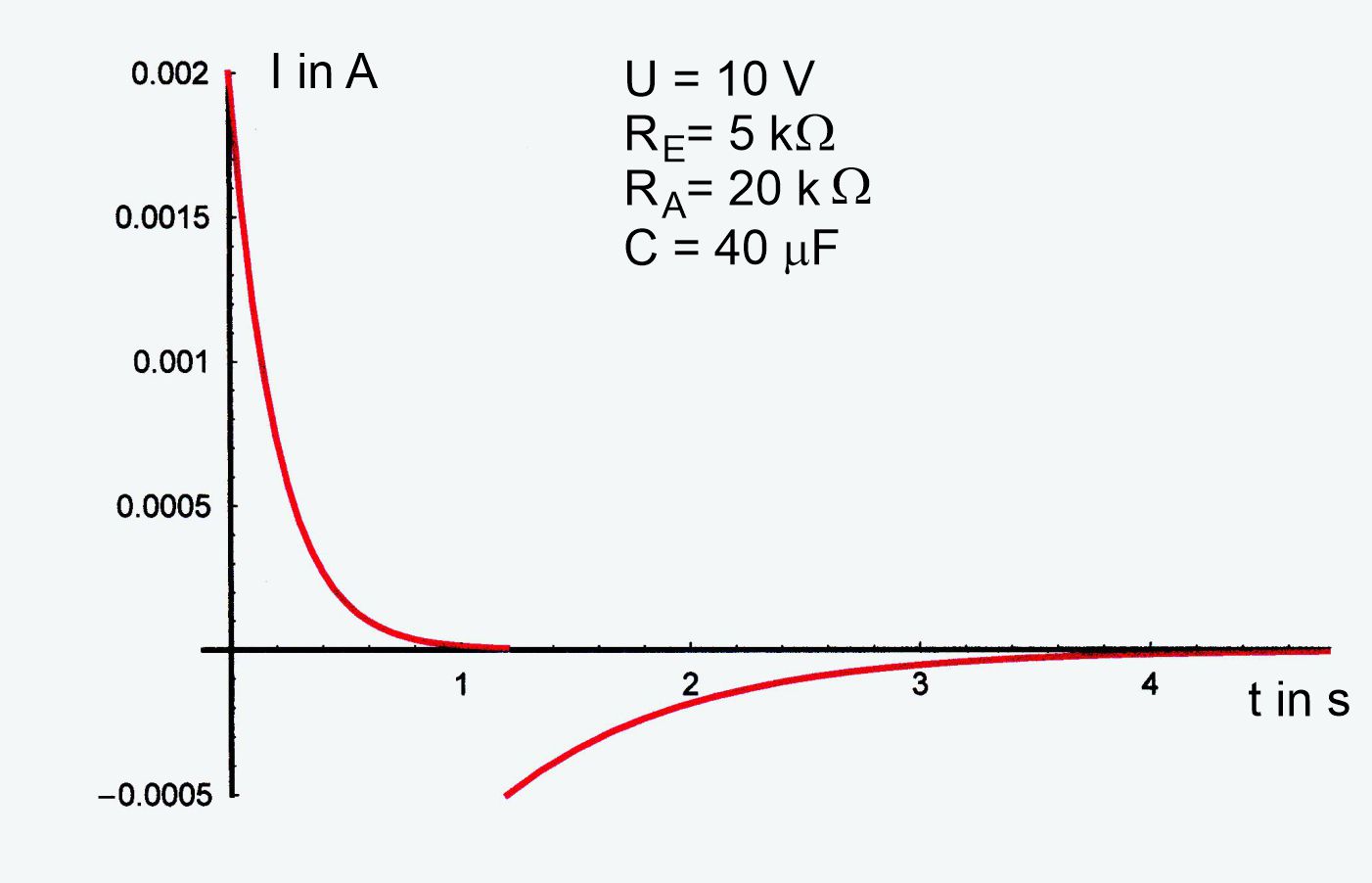
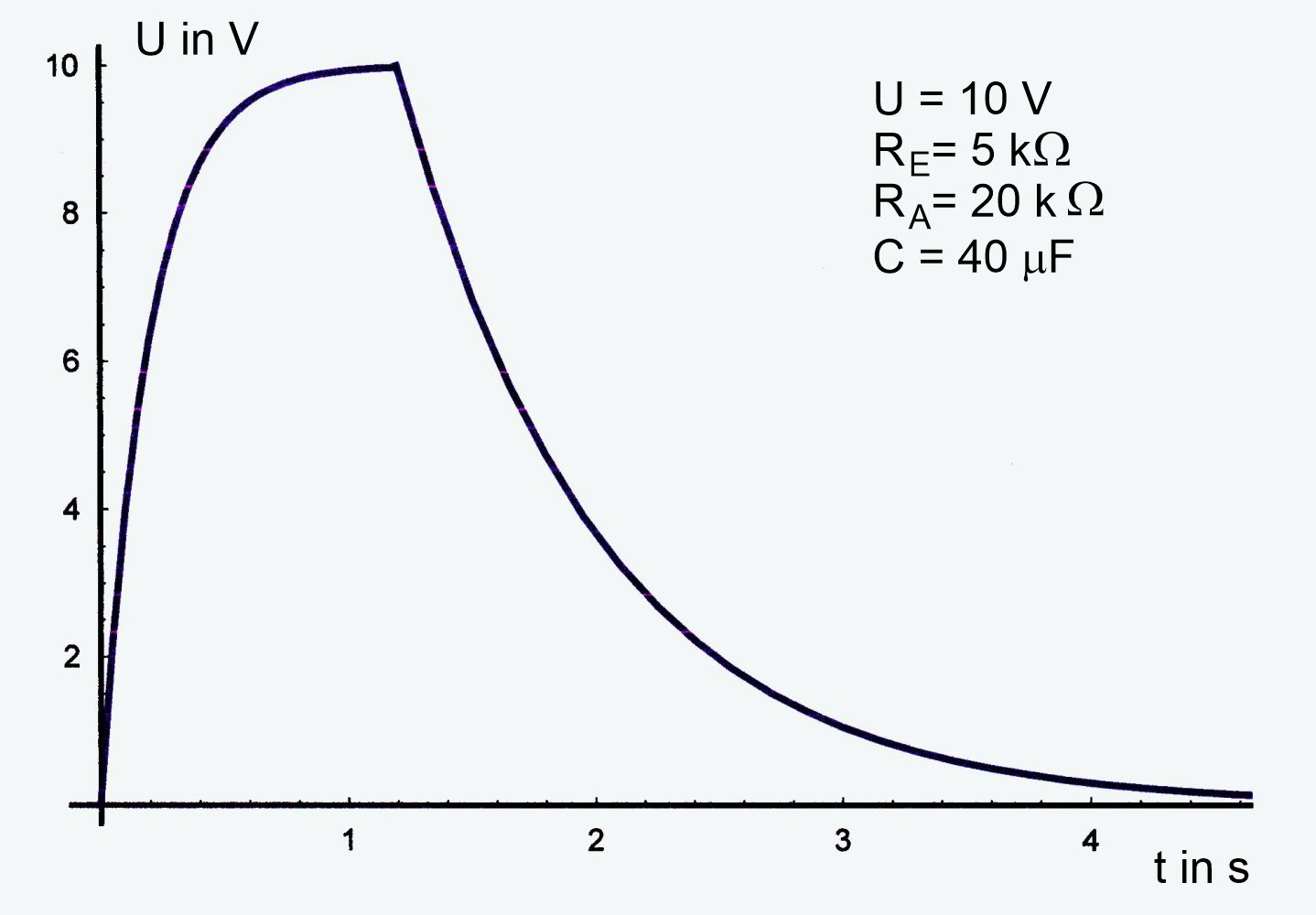
2. Fall. Ein- und Ausschaltwiderstand sind
unterschiedlich. Bei größerem Ausschaltwiderstand dauert es länger
bis die Ladungen ab- fließen.
gehe zu: zurück zu Kapitel weiter zu Kapitel zur Übersicht: Felder Induktion |