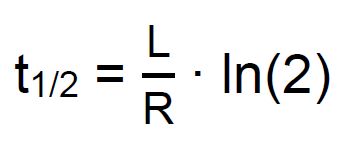Abituraufgaben

Aufgabe Nr.2 (LK)

Vorgegeben ist eine Spule der Induktivität L, eine Spannungsquelle

U₀ und ein ohmscher Widerstand R. Die Bauelemente sind ent-

sprechend der Schaltskizze verbunden. Über den Wechselschalter S

kann die Spule wahlweise kurzgeschlossen oder mit der Batterie ver-

bunden werden.

a.) Der Schalter wird zur Zeit t = 0 s in Stellung a geschlossen.

Der zeitliche Verlauf der Stromstärke (Ladestrom) wird gemessen.

Die Tabelle zeigt die Messreihe.

t in s	0,6	1,3	1,9	2,8	3,6	4,4	5,5	6,9	9,4	14,4
I in mA	0,15	0,3	0,42	0,53	0,6	0,7	0,76	0,84	0,93	0,97

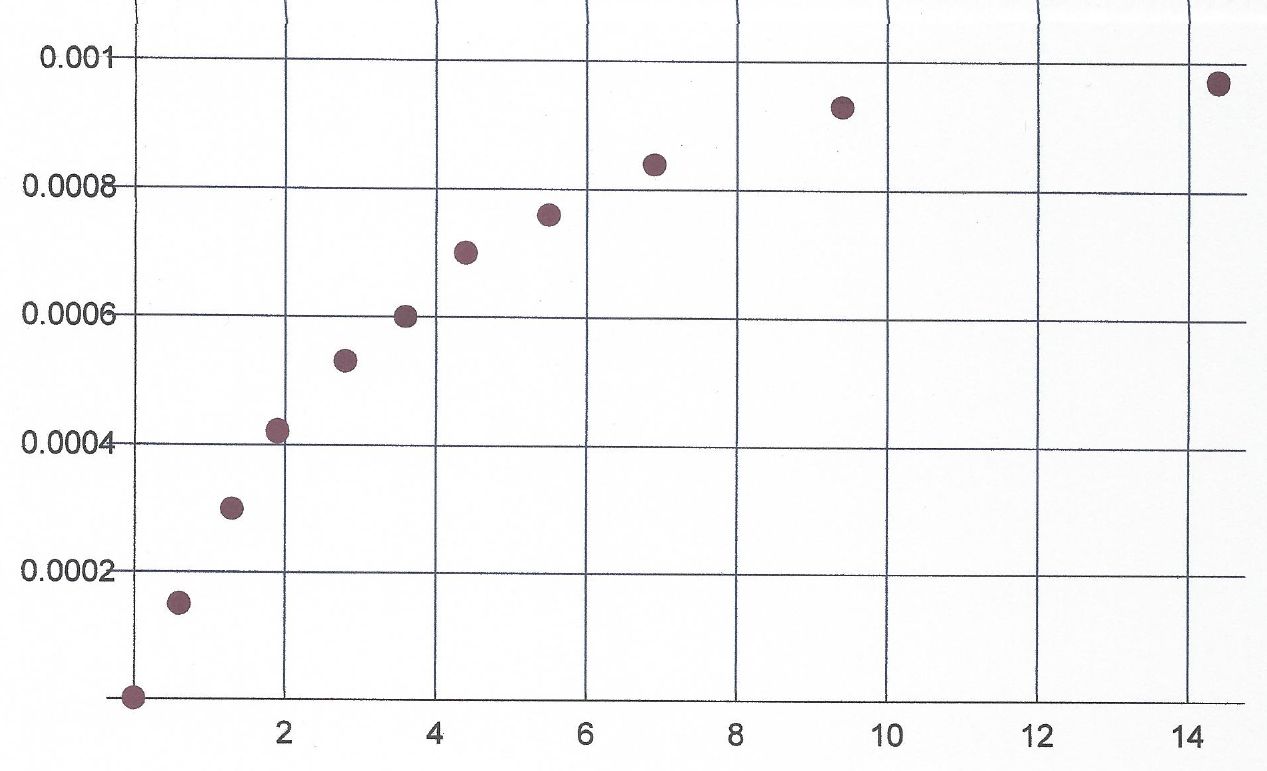
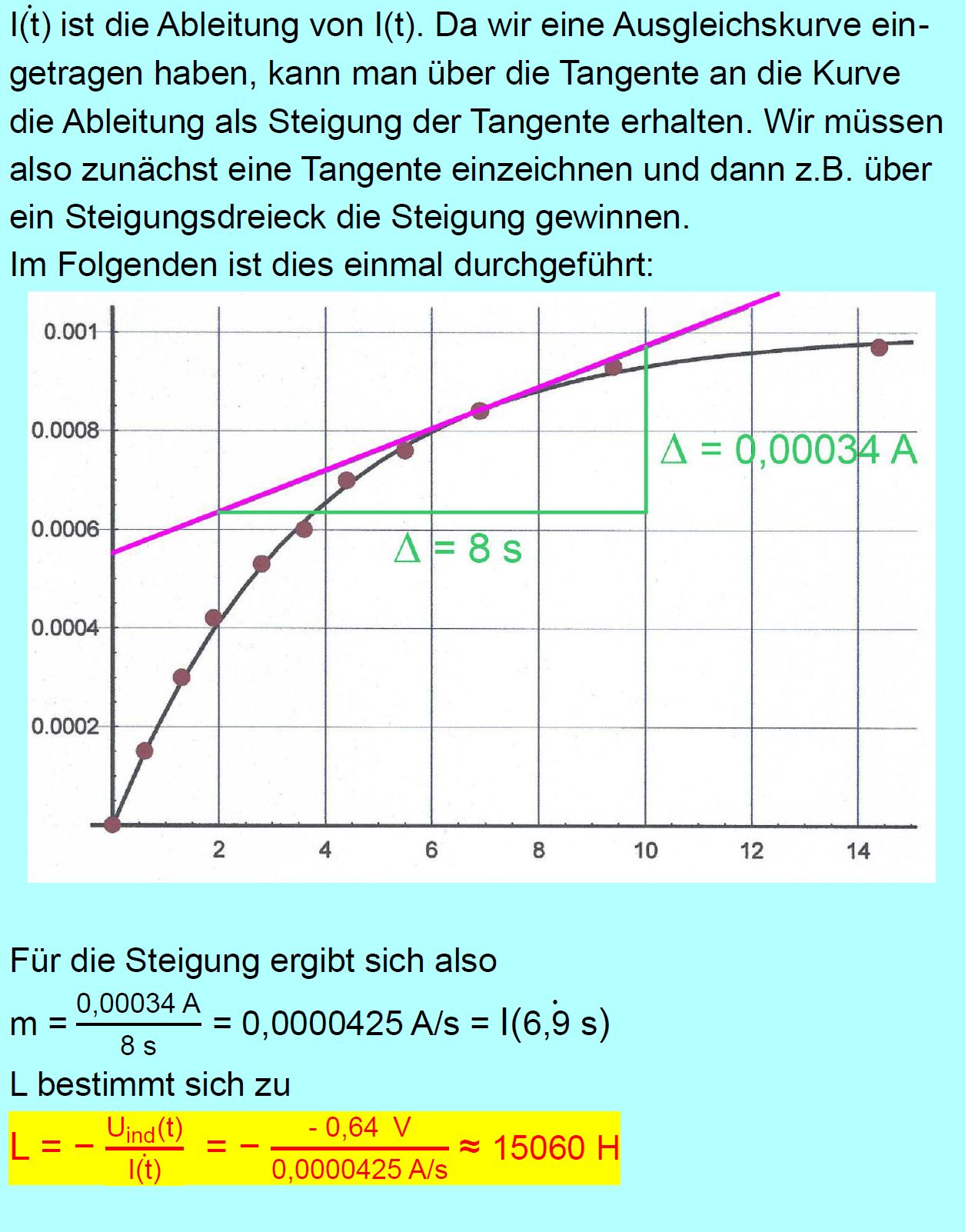
1.) Stellen Sie die Messwerte graphisch dar [ x-Achse: t, y-Achse: I ].

2.) Beschreiben Sie den graphischen Verlauf. Erläutern Sie aus

physikalischer Sicht, wie es zu diesem Verlauf kommt.

b.) Bestimmen Sie aus dem Graphen den Widerstand R des Strom-

kreises (U₀ = 4 V) und die Induktivität der Spule. Erläutern Sie ihr

Verfahren ausführlich.

Hinweis:

1.) Für die Spannung gilt die Maschenregel, also U(t) = U₀ + U_ind(t)

[U(t) = Spannung am ohmschen Widerstand; U_ind(t) = Induktionsspannung der

Spule]

2.) Die maximale Stromstärke sei I (t = ∞ s) = I_max = 0,001 A

c.) Leiten Sie einen Funktionsterm für I (t) her (allgemeiner Fall).

Benutzen Sie den Hinweis aus b.) mit

Zur Kontrolle:

.

d.) Unter der Annahme, dass der Strom I (t) bei der Spannung U_E

einen Wert I_E erreicht hat, wird der Schalter S ideal (d.h. ohne Zeit-

verzögerung) in Stellung b gebracht (t = 0 s). Für die Entlade-

stromfunktion I (t) gilt dann

1.) Leiten Sie diese Gleichung her (Ansatz aus b.) mit U₀ = 0 V.

2.) Skizzieren Sie den Verlauf des Graphen dieser Funktion.

3.) Leiten Sie für die Halbwertszeit die folgende Formel her:

e.) In einem Stromkreis der oben abgebildeten Art gelten folgende

Bedingungen:

R = 4000 Ω, L = 15 000 H, U₀ = 4 V. Berechnen Sie die Stromstärke

zum Zeitpunkt t = 15 s, wenn mit t = 0 s der Ladevorgang (siehe a.))

beginnt und nach 10 s ideal umgeschaltete wird (siehe d.)).

Lösungen:

zu a.)

Graphischer Verlauf (Wertepaare)

Graphischer Verlauf mit Ausgleichskurve:

Beschreibung:

starker Anstieg, der sich immer mehr abflacht; man spricht

von einer Sättigungskurve; die Kurve nähert sich von unten

einer Waagerechten; nach den Vorgaben liegt diese Gerade

bei I = 0,001 A = I_max; die Kurve hat einen Funktionsterm der

Form I(t) = I_max ∙ ( 1 − e^{− k ∙ t} ), mit größerem t wird e^{− k ∙ t} immer

kleiner, strebt also gegen Null; bei t = 0 s ist e^{− k ∙ t} = 1, somit

I(0) = 0 A; für t → ∞ gilt für e^{− k ∙ t} → 0, also I(t) → I_max

Erläuterung (Physik):

Das Einschalten sorgt für den Aufbau eines Magnetfeldes in

der Spule; da jetzt eine Stromstärke durch die Spule fließt, die

Stromstärkeänderung ist extrem groß, so dass U_ind auch sehr

groß ist, es gilt ja U_ind(t) = − L ∙ I‘(t), so dass U(t≈0s) ≈ 0 V ist

und somit I(t≈0s) ≈ 0 A;

bei Erhöhung von t gibt es weiterhin eine Stromstärkeänder-

ung, so dass U_ind auftritt und U₀ entgegenwirkt;

die Stromstärkeänderung nimmt mit der Zeit ab, so dass auch

U_ind(t) geringer wird, somit nimmt U(t) und somit I(t) zu;

Hinweis:

Die exakten Formeln (s. digitales Physikbuch) lauten

c.)

Die Herleitung ist in einem Kapitel des „digitalen Physikbuchs“

erfolgt (Link) und wird hier übernommen.

Es ist gut, wenn man als Voraussetzung folgendes weiß,

sonst kann man sich die Herleitung auch in dem genannten

Kapitel nachlesen.

d.) 1.)

Herleitung ebenfalls im „digitalen Physikbuch“ erfolgt (LINK).

d.) 3.)

Herleitung wie im „digitalen Physikbuch“ (LINK):

zurück zum Kapitel „Selbstinduktion−Einschalten“

zurück zur Übersicht „Induktion“
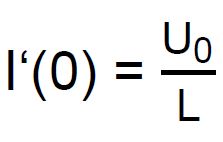
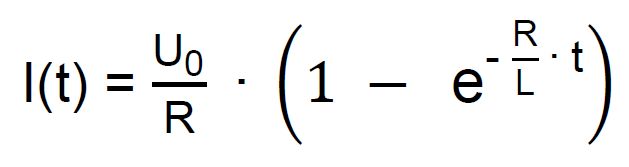